Дифференциаль исәпләү

Дифференциаль исәпләү — математик анализның чыгарылма һәм дифференциал төшөнчәләре һәм аларны функцияләрне тикшерү өчен куллану ысуллары өйрәнелгән бүлеге. Дифференциаль исәпләүнең төзелүе Исаак Ньютон һәм Готфрид Лейбниц исемнәре белән бәйле. Нәкъ алар төп кагыйдәләрне төгәл әйтеп бирәләр һәм дифференциальләү һәм интегральләунең үзара кире характерын билгелиләр. Дифференциаль исәпләүне төзү (интеграль исәпләү белән бергә) математика үсешендә яңа чор асты. Моның белән рәтләр теориясе, дифференциаль тигезләмәләр теориясе һәм башкалар кебек күп фәннәр бәйле. Математик анализ ысуллары математиканың бөтен бүлекләрендә дә куллану таптылар. Математиканы табигать фәннәрендә һәм техникада куллану өлкәсе киң тарала. Дифференциаль исәпләү математиканың, билгеләмәсе һәм өйрәнүе математик анализга башлангыч темасын тәшкил иткән шундый мөһим төшөнчәләргә нигезләнә: чын саннар (санлы туры сызык), функция, чик, өзлексезлек. Бөтен бу төшөнчәләр дифференциаль һәм интеграль исәпләүләрнең үсеше һәм ныгынуы барышында хәзергәчә аңлату алдылар. Дифференциаль исәпләүнең төп идеясе функцияны бәләкәйдә өйрәнүдән тора. Тәгаенрәк әйткәндә дифференциаль исәпләү, һәр ноктасының җитәрлек бәләкәй якын тирәсендә үз-үзен тотышы сызыкча функциянең яки күпбуынның үз-үзен тотышына якын булган функцияләрне өйрәнү өчен аппарат бирә. Шундый аппарат булып дифференциаль исәпләүнең үзәк төшенчәләре тора: чыгарылма һәм дифференциал.

Дифференциаль исәпләү
Өйрәнелгән тармак	функция чыгарылмасы
Нинди вики-проектка керә	Проект:Математика[d]
ACM коды (2012)	10003734
Моның каршысы	Интеграль хисап
Дифференциаль исәпләү Викиҗыентыкта

Бер үзгәрүчәнле функцияләрнең дифференциаль исәпләве

Чыгарылма

$g(h)$ функциясе $h=0$ якын тирәсендә бирелсен ди һәм теләсә нинди $\epsilon$ > 0 өчен шундый $\delta$ табылсын, монда

$|h|<\delta$ булу белән $|g(h)/h^{n}|<\epsilon ,$

ул чакта $g(h)$ — $o(h^{n})$ тәртиптәге чиксез бәләкәй дип әйтәләр. $f(x)$ — $(a,b)$ кисәгендә бирелгән чын кыйммәтле функция булсын ди. Бу функцияне, әгәр теләсә нинди $x\in (a,b)$ һәм теләсә нинди $n$ өчен

$f(x+h)=f(x)+f'(x)h+{\frac {1}{2!}}f''(x)h^{2}+\dots {\frac {1}{n!}}f^{(n)}(x)h^{n}+o(h^{n})$ булса, $(a,b)$ интервалында чиксез дифференциалланучы дип атыйлар.

Шулай итеп, локаль, кисемтәнең теләсә нинди ноктасының якын тирәсендә функция күпбуын белән теләсә күпме якшы якыная. $(a,b)$ кисемтәсендә шома функцияләр $C^{\infty }(a,b)$ шома функцияләр боҗрасын төзи. $f^{(n)}(x)$ коэффициентлары

$f^{(m)}(x+h)=f^{(m)}(x)+f^{(m+1)}(x)h+\dots {\frac {1}{n!}}f^{(m+n)}(x)h^{n}+o(h^{n})$

Бу функцияләрны $f(x)$ функциясенең чыгарылмасы дип атыйлар. Беренче чыгарылма чикләнмә кебек исәпләнергә мөмкин.

$f'(x)=\lim \limits _{h\to 0}{\frac {f(x+h)-f(x)}{h}}$.

$f(x)$ функциясенә аның $f'(x)$ чыгарылмасын ярашлы куйган операторы

$D={\frac {d}{dx}}$ дип тамгалыйлар.

Шуның белән бергә ике шома f һәм g функцияләре өчен

$D(f+g)=Df+Dg$ һәм $D(fg)=fDg+gDf$ дөрес.

Шундый үзенчәлекләргә ия булган операторны шома функцияләр боҗрасын дифференциальләү дип атыйлар. $(a,b)$ кисемтәсендә голоморфлы һәр аналитик функция шома функция була, ләкин киресе дөрес түгел. Аналитик һәм шома функцияләрнең төп аермасы шунда, беренчеләре тулысынча бер ноктаның якын тирәсендәге үз-үзен тотышы белән билгеләнәләр, икенчеләре — юк. Мәсәлән, шома функция бер ноктаның ян-ягында даими булырга мөмкин, ләкин бөтен җирдә даими булмаска мөмкин. Элементар функцияләр үзләренең (ачык) билгеләнү өлкәсендә аналитик булалар, димәк, шома функция да булалар. Ләкин, аналитик функцияләрдән аермалы рәвештә, шома функцияләр төрле интервалларда төрле элементар аңлатмалар белән бирелергә мөмкиннәр.

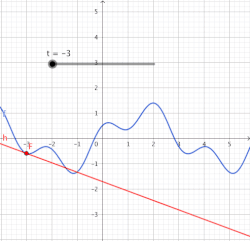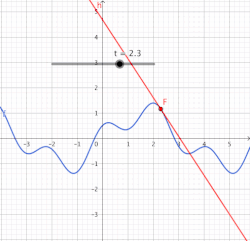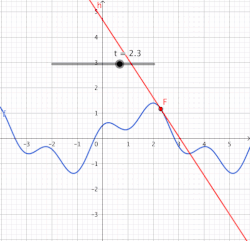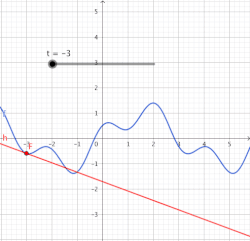
Тиюче туры сызык

Функциянең графигы (кара кәкре сызык) һәм тиюче туры сызык (кызыл туры сызык)

$y=f(c)+f'(c)(x-c)$ туры сызыгы

$y=f(x)$ кәкре сызыгын

$(c,f(c))$ ноктасында шулай итеп кисеп үтә, монда

$f(x)-f(c)-f'(c)(x-c)={\frac {1}{2}}f''(c)(x-c)^{2}+o((x-c)^{2})$ аңлатмасының тамгасы

$f''(c)\not =0$ шарты үтәлгәндә һәрвакыт бер үк кала, шуңа күрә дә

$y=f(x)$ кәкре сызыгы

$y=f(c)+f'(c)(x-c)$ туры сызыгынан бер якта ята.

Күрсәтелгән үзенчәлеккә ия булган туры сызыкны кәкре сызыкка $x=c$ ноктасында тиюче туры сызык дип атыйлар (Б. Кавальери буенча).

$y=f(x)$ кәкре сызыгының

$y=f(c)+f'(c)(x-c)$ туры сызыгынан бер якта ятмаган $x=c$ ноктасын бөгөлү ноктасы дип атыйлар, шуның белән бергә туры сызыкны барыбер тиюче туры сызык дип атыйлар. Бер төрлелек өчен тиюче туры сызык төшенчәсенең үзен, ике очрак та аңа туры килсен өчен, икенче төрле кертәләр.

Экстремум нокталары

$x=c$ ноктасы Локаль максимум (минимум) ноктасы дип атала, әгәр бөтен модуле буенча җитәрлек бәләкәй $h$ өчен

$f(c)-f(c+h)>0\quad (f(c)-f(c+h)<0)$ булса.

$f'(c)h+{\frac {1}{2}}f''(c)h^{2}+o(h^{2})<0$ нисбәтеннән шунда ук $f'(c)=0$ — максимумның кирәкле шарты, ә $f''(c)<0$ — максимумның җитәрлек шарты икәне күренә. $f''(c)=0$ шарты максимум, минимум һәм бөгелү нокталарын аера.

Өзлексез функцияләр

$f$ функциясе $[a,b]$ интервалының очларында да бирелсен, ди; $f$ функциясе $[a,b]$ кисемтәсендә өзлексез дип әйтәләр, әгәр теләсә нинди $\epsilon$ өчен шундый $\delta$ табылса, монда

$|h|<\delta$ шарты үтәлү белән $|f(x)-f(x+h)|<\epsilon$ булса,

һәм $x,\,x+h$ нокталары $[a,b]$ интервалы тышына чыкмаса. Вейерштрасс теоремасы, кисемтәдә шома функция бу кисемтәдә үзенең минималь һәм максималь кыйммәтләрен кабул итә дип раслый. Функциянең өзлексезлек төшөнчәсе гадәттә функциянең чикләмәсе төшенчәсе белән бәйләнә. $[a,b]$ интервалында өзлексез функцияләр $C[a,b]$ өзлексез функцияләр боҗрасын төзи.

Тарихы

XII гасырда Хулагу төрөк-монгол дәүләтенең математигы Шәрәфетдин ат-Туси, дифференциаль исәпләүдә мөһим нәтиҗә булган куб функциясенең чыгарылмасын беренче булып таба. «Трактат об уравнениях» хезмәтен яза, анда уңай чыгарылышы булмаган куб тигезләмәләрне чыгару өчен, дифференциаль исәпләү белән бәйле, функциянең чыгарылмасы һәм кәкре сызыкның максимумнары һәм минимумнары кебек концепция эшли.

Дифференциаль исәпләүнең төп теоремалары

$[a,b]$ кисемтәсендә өзлексез һәм $(a,b)$ интервалында шома функцияләр боҗрасы берничә мөһим үзенчәлеккә ия:

• Ролль теоремасы: $f(a)=f(b)$ булса, ул чакта $c\in (a,b)$ максимум яки минимум ноктасы бар, анда $f'$ нульгә әйләнә.
• Лагранж теоремасы: шундый $c\in (a,b)$ ноктасы бар, аның өчен

${\frac {f(b)-f(a)}{b-a}}=f'(c)$ үтәлә.

• Коши теоремасы: әгәр $(a,b)$ интервалында $g'\not =0$ булса, ул чакта шундый $c\in (a,b)$ ноктасы бар, аның өчен

${\frac {f(b)-f(a)}{g(b)-g(a)}}={\frac {f'(c)}{g'(c)}}$

Лагранж теоремасыннан Лагранж формасында калдык буын белән Тейлор формуласын чыгаралар: теләсә нинди $(a',b')\subset (a,b)$ кисемтәсендә шундый $c_{n}$ нокталары бар, монда

$f(b')=f(a')+f'(a')(b'-a')+{\frac {1}{2!}}f''(a')(b'-a')^{2}+\dots {\frac {1}{n!}}f^{(n)}(a')(b'-a')^{n}+R_{n}$

монда

$R_{n}={\frac {1}{(n+1)!}}f^{(n+1)}(c_{n})(b'-a')^{n+1}$

Бу формула ярдәмендә, функциянең һәм аның чыгарылмаларының $a'$ ноктасындагы билгеле кыйммәтләре буенча, функциянең $b'$ ноктасындагы кыйммәтен якынча исәпләргә мөмкин. Коши теоремасыннан Лопиталь кагыйдәсен чыгаралар: әгәр $f(b)=g(b)=0$ яки $f(b)=g(b)=\infty$, һәм $(a,b)$ интервалында $g'\not =0$ булса, ул чакта

$\lim \limits _{x\rightarrow b-0}{\frac {f(x)}{g(x)}}=\lim \limits _{x\rightarrow b-0}{\frac {f'(x)}{g'(x)}},$

шулай ук икенче чикләнмәнең булуы беренчесенең булуын китереп чыгара.

Шулай ук карагыз

• Вариацион исәпләү
• Күп үзгәрүчәнле функцияләр анализы
• Интеграль исәпләү
• Математик анализ
• Коммутатив алгебралар өстендә дифференциаль исәпләү

Әдәбият

• Дифференциальное исчисление // Брокгауз һәм Ефрон энциклопедик сүзлеге: 86 томда (82 том һәм 4 өстәмә). Санкт-Петербург: 1890—1907.

• Виноградов И.М. (ред.) Математическая энциклопедия. Том 2. Москва: Советская энциклопедия, 1977 г.
• Бронштейн И. Н., Семендяев К. А., Справочник по математике для инженеров и учащихся втузов. М.: Наука, 1981 год.