Охшашлык

Охшашлык — теләсә нинди ике $A$, $B$ нокталары һәм аларның образлары $A'$, $B'$ һәм охшашлык коэффициенты дип аталган ниндидер $k\neq 0$ саны өчен $|A'B'|=k\cdot |AB|$ нисбәте үтәлгән Евклид пространствосын үзгәртү ул.

Охшаш турыпочмаклыклар

Тарихы

Охшаш фигуралар Борынгы Грециядә безнең эрага кадәр V—IV гасырларда каралган; алар Гиппократ Хиосский, Архит Тарентский, Евдокс Книдский хезмәтләрендә һәм Евклидның «Башлангычлар»ының VI китабында очрый.

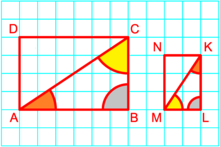
Мисаллар

• Теләсә нинди гомотетия охшашлык була.
• Теләсә нинди хәрәкәтне (шул исәптән тождествоны) шулай ук $k=1$ коэффициенты белән охшашлык үзгәртүе дип карарга була.

Бәйле билгеләмәләр

• Әгәр $F\mapsto F'$ булган охшашлык үзгәртүе булса, $F$ фигурасы $F'$ фигурасына охшаш дип атала.
  • Фигураларның охшашлыгы эквивалентлылык бәйләнеше була.
  • Охшашлыкны тамгалау өчен $\sim$ — тамгасы кулланыла, $F$ һәм $F'$ фигуралары охшаш дигәнне $F\sim F'$ дип язып була.

Охшашлык ысулы

Фигуралар охшашлыгы бик күп төзүгә мәсьәләләр эшләүгә ярдәм итә. Охшашлык ысулы шуннан тора, мәсьәләдәге кайсыбер бирелешләр буенча башта эзләнгән фигурага охшаш фигура төзиләр, ә азак эзләнгән фигурага күчәләр. Бу ысул, бер генә бирелгән зурлык озынлык, ә калганнары — я почмаклар, я кисемтәләр чагыштырмасы булган очракта бигрәк тә уңайлы. Охшашлык ысулына мәсьәләнең классик мисалы булып, бирелгән почмакның ике ягына тиюче һәм бирелгән нокта аша үтүче әйләнә төзү тора

Үзенчәлекләре

• Охшашлык Евклид пространствосын үзенә үз-ара бер мәгънәле чагыштыру була.
• Охшашлык ясылыкны аффинналы үзгәртү була.
• Охшашлык туры сызыкта нокталарның урнашу тәртибен саклый, ягъни әгәр $B$ ноктасы $A$ һәм $C$ нокталары арасында ятса һәм $B'$, $A'$, $C'$ — ниндидер охшашлыкта аларның ярашлы образлары булса, ул чакта $B'$ ноктасы шулай ук $A'$ һәм $C'$ нокталары арасында ята.
• Бер туры сызыкта ятмаган нокталар, теләсә нинди охшашлыкта, бер туры сызыкта ятмаган нокталарга күчәләр.
• Охшашлык туры сызыкны туры сызыкка, кисемтәне кисемтәгә, нурны нурга, почмакны почмакка, әйләнәне әйләнәгә күчерә.
• Охшашлык кәкре сызыклар арасындагы почмак зурлыгын саклый.
• Коэффициенты $k\not =1$ булган охшашлык, теләсә нинди туры сызыкны аңа параллель булган туры сызыкка чагылдыра, $k$ яки $-k$ коэффициенты белән гомотетия була.
  • Һәр охшашлыкны $D$ хәрәкәте белән ниндидер уңай коэффициентлы $\Gamma$ гомотетиянең композициясе итеп карарга була.
  • Охшашлык үз (үз түгел) дип атала, әгәр $D$ хәрәкәте үз (үз түгел) булса. Үз охшашлык фигураларның ориентациясен саклый, ә үз булмаганы — ориентацияне капма-каршыга үзгәртә.
• Ике өчпочмак охшаш була, әгәр
  • аларның ярашлы почмаклары тигез булса, яки
  • яклары пропорциональ булса. Шулай ук карагыз - Өчпочмакларның охшашлык билгеләре.
• Охшаш фигураларның мәйданнарының чагыштырмасы аларның охшаш сызыкларының (мәсәлән, якларының) квадратларына пропорциональ. Шулай, түгәрәкләрнең мәйданнары аларның радиуслары квадратлары чагыштырмасына пропорциональ.

Гомумиләштерү

3-үлчәмле Евклид пространствосында охшашлык шулай ук билгеләнә ( югарыда карап кителгән үзенчәлекләре саклана), һәм шулай ук n-үлчәмле Евклид һәм псевдоевклид пространствосында. Үлчәмле пространстволарда, $n$-үлчәмле Риманов, псевдориманов һәм Финслер пространстволарындагы кебек, охшашлык пространствоның үлчәмен үз-үзенә даими тапкырлаучыга кадәр тәгаенлек белән күчерүче үзгәртү сыман билгеләнә. n-үлчәмле Евклид, псевдоевклид, Риманов, псевдориманов яки Финслер пространстволарының бөтен охшашлыклары җыелмасы, ярашлы пространствоның охшашлык (гомотетик) үзгәртүләр төркеме дип аталган, $r$-буынлы Ли үзгәртүләре төркемен төзи. Күрсәтелгән типтагы һәр пространствода $r$-буынлы Ли охшашлык үзгәртүләре төркемендә хәрәкәтләрнең $(r-1)$-буынлы нормаль астөркеме бар.

Шулай ук карагыз

• Өчпочмакларның охшашлык билгеләре
• Конгруэнтлык (геометрия)
• Конформлы чагылыш
• Симметрия
• Үзохшашлык

Сылтамалар

• Равенство и подобие геометрических фигур.
• Гомотетические фигуры // Брокгауз һәм Ефрон энциклопедик сүзлеге: 86 томда (82 том һәм 4 өстәмә). Санкт-Петербург: 1890—1907.